Emotrasfusione : Emoglobina o Emogasanalisi?
Quale è la concentrazione di emoglobina a cui è opportuno fare una trasfusione di emazie?
C’è un largo consenso, ripreso anche dalle linee guida (1), nell’identificare come soglia di trasfusione un valore di emoglobina di 7 g/dL. Numerosi studi hanno infatti dimostrato che la trasfusione di emazie per concentrazioni di emoglobina più elevate rispetto a questa soglia non dà vantaggi in termini di mortalità a breve o lungo termine, durata della degenza o disfunzioni d’organo (2-6).
La risposta alla domanda iniziale sembra quindi chiara … ma se riflettiamo bene questa risposta ci dice come risparmiare emoderivati, non quando la trasfusione di emazie apporta un beneficio al paziente.
Come sempre la qualità della risposta dipende dalla qualità della domanda: visto l’esito della risposta, probabilmente non è una buona domanda chiedersi quale sia il valore giusto di concentrazione dell’emoglobina per decidere una trasfusione.
La fisiologia ci aiuterà a capire quale possa essere la “domanda giusta” per trasfondere emazie con un beneficio clinico. Successivamente cercheremo la risposta a questa domanda nei dati che possiamo trovare nella ricerca clinica.
Guida fisiologica alla “domanda giusta”.
Trasporto e consumo di ossigeno.
Fisiologicamente un soggetto a riposo consuma circa 250 ml di O2 ogni minuto (V˙O2V˙O2). Il V˙O2V˙O2 è garantito dal trasporto di ossigeno ai tessuti (oxygen delivery, DO2), un magnifico lavoro di squadra degli apparati respiratorio e cardiocircolatorio: il primo ”carica” il sangue di ossigeno, il secondo lo fa arrivare ai tessuti. Il DO2 è il prodotto del contenuto di ossigeno del sangue arterioso (CaO2) e della portata cardiaca (cardiac output, CO):
Se si vuole raggiungere un DO2 di 250 ml di O2/min, esattamente uguale al V˙O2V˙O2, l’equazione diventa:
In assenza di emoglobina servirebbe una portata cardiaca di almeno 83 l/min per garantire l’apporto fisiologico di 250 ml/min di O2 ai tessuti. In altre parole, in assenza di emoglobina un elevatissimo CO dovrebbe sopperire al bassissimo CaO2.
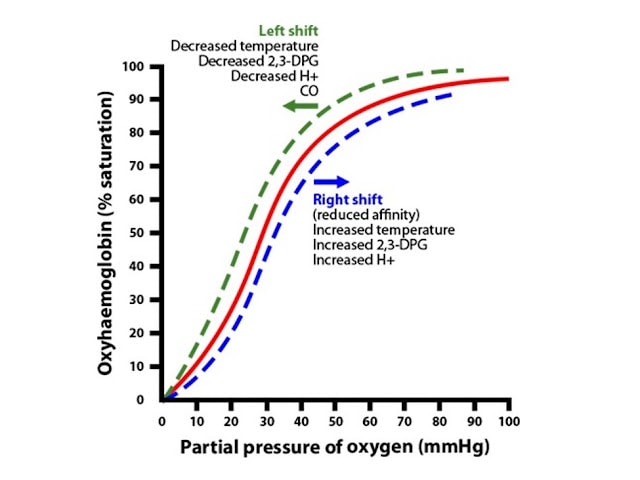
Per fortuna abbiamo l’emoglobina, che aumenta enormemente il CaO2 legando a sè moltissimo ossigeno, il quale si va ad aggiungere all’ossigeno disciolto nel sangue. Ogni grammo di emoglobina può legare un massimo di 1.39 ml di O2 se tutti i siti di legame per l’O2 sono occupati da una molecola di ossigeno. Questa è la condizione che conosciamo come saturazione 100%. Tanto più elevata è la PaO2, tanto maggiore è la saturazione dell’emoglobina, con una relazione espressa dalla ben nota curva di dissociazione dell’emoglobina.
Una PaO2 di 95 mmHg fisiologicamente si associa ad una saturazione del 97%, che significa che il 97% dei siti di legame dell’emoglobina per l’ossigeno sono legati ad una molecola di O2.
In questa condizione il CaO2 con una ipotetica concentrazione di emoglobina di 10 g/dL diventerebbe:
Estrazione di ossigeno.
La portata cardiaca fisiologica è più del triplo di questo valore (circa 5.6 l/min), questo consente all’organismo di trasportare oltre il triplo dell’ossigeno necessario alle necessità del metabolismo cellulare. Riprendendo l’equazione 1:
L’estrazione di ossigeno (O2 extraction ratio, O2ER) esprime la proporzione dell’ossigeno trasportato che viene utilizzato dal metabolismo tissutale, cioè il rapporto tra V˙O2V˙O2 e DO2:
Da questi due esempi possiamo capire l’importanza del O2ER nel contribuire in maniera fondamentale alla decisione di trasfondere o meno emazie. Nel primo caso potremmo trasfondere il paziente per aumentare il DO2 ed allontanarlo dalla soglia del debito di ossigeno, nel secondo caso invece la trasfusione apparirebbe inutile da questo punto di vista.
Vediamo infine un ultimo esempio in cui la valutazione del O2ER ci può suggerire di trasfondere emazie anche con un’emoglobina di 10 g/dL. Se un paziente avesse un aumento del V˙O2V˙O2 a 300 ml/min ed una portata cardiaca ridotta a 4.5 l/min (anche questi dati ragionevoli per un paziente in Terapia Intensiva), la O2ER sarebbe 0.48 nonostante l’emoglobina a 10 g/dL: a questo valore di O2ER potrebbe avere un razionale la trasfusione di emazie (soprattutto se non fosse possibile ridurre il V˙O2V˙O2 o aumentare il CO).
La risposta alla “domanda giusta”: come misurare il O2ER con l’emogasanalisi.
La strada più lunga.
La differenza CaO2 – CvO2 è conosciuta anche come differenza artero-venosa di O2 (Ca-vO2). Utilizzando il V˙O2V˙O2 ricavato dall’equazione 9, abbiamo gli strumenti per capire come calcolare O2ER dai dati dell’emogasanalisi arteriosa e venosa:
Ipotizziamo di avere un paziente con 10 g/dL di emoglobina, PaO2 95 mmHg, SaO2 97%, SvO2 67% e PvO2 di 36 mmHg e calcoliamo il suo O2ER:
La strada più breve.
Semplificando ulteriormente, l’equazione 12 mostra che, se la SaO2 è 100%, la SvO2 è inversamente proporzionale al O2ER. Infatti:
Gli studi clinici.
La fisiologia ci fa capire che la trasfusione di emazie dovrebbe avere l’obiettivo di adeguare la DO2 al V˙O2V˙O2, ed il O2ER è l’indicatore più appropriato. La concentrazione dell’emoglobina, quella che solitamente si guarda per decidere se trasfondere emazie, dovrebbe essere invece un elemento secondario alla valutazione delO2ER.
Uno studio clinico fornisce una indiretta conferma a questo ragionamento fisiologico (9). Lo studio ha analizzato 177 pazienti in Terapia Intensiva con emoglobina tra 7 e 10 g/dL. Questi pazienti anemici potevano essere trasfusi o non trasfusi a giudizio del medico curante. In tutti i pazienti, indipendentemente dalla decisione di trasfondere emazie, furono calcolati sia il Ca-vO2 (la differenza artero-venosa di contenuto di ossigeno) sia il O2ER.
Conclusioni.
- l’emotrasfusione dovrebbe essere presa in considerazione in tutti i pazienti anemici. La soglia dell’anemia è arbitraria ma possiamo porla orientativamente a 10 g/dL di emoglobina;
- nei pazienti anemici si dovrebbe valutare il O2ER, calcolato facilmente come (SaO2-SvO2)/SaO2;
- un O2ER < 0.3 dovrebbe avvalorare la decisione di non trasfondere, anche se l’emoglobina fosse un po’ inferiore a 7 g/dL;
- un O2ER > 0.3:
- supporterebbe l’indicazione alla trasfusione come primo intervento terapeutico in caso di anemia grave (arbitrariamente definita con un valore di emoglobina inferiore a 7 g/dL);
- nei pazienti con anemia moderata (emoglobina superiore a 7 g/dL) la trasfusione di emazie sarebbe comunque indicata dopo una ragionevole ottimizzazione di portata cardiaca e consumo di ossigeno.